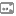Eternal InflationThe mechanism through which primordial inhomogeneities are produced in inflation is truly remarkable. Simple models of inflation involve a scalar field φ rolling down the hill provided by its assumed potential energy function V(φ). As long as V(φ) is positive, it acts like a positive cosmological constant which causes exponential expansion of the Universe. However, the field φ, like every other field, is subject to quantum mechanical fluctuations. As it rolls down the hill, in some regions φ fluctuates downwards and in others it fluctuates upwards. The former regions reach the bottom of the hill, and convert the energy stored in φ into hot radiation sooner: the latter regions do so later. Since the density of the radiation rapidly decreases as the universe expands, the regions undergoing heating later are left with a higher energy density than those undergoing heating sooner. This is a very beautiful idea, because it links gravity to quantum mechanics and in fact provides one of our few observational probes of quantum gravity. All the more remarkable is that it appears to be consistent with the latest observational data. If this is the correct explanation of the origin of structure in the Universe, then quantum processes were crucial to the formation of the Universe we now see. The naive approach to inflation begs the question of why the scalar field started out up the hill. Of course that was necessary in order to get inflation going, but assuming that is really just assuming the desired answer. The mechanism of quantum fluctuations offers an intriguing way out of this impasse which has been seized upon by Guth and others. The idea is that those regions in which the field jumps uphill will not only undergo heating later, but they will actually undergo inflation for longer. Since inflation is exponentially powerful, regions undergoing inflation for longer expand to vastly greater size. The thought is therefore that in large parts of the Universe they will have quantum jumped uphill, and these parts will multiply. Within these exponentially growing regions, small ‘island Universes’ will appear in which the field does roll down the hill and releases its energy into hot radiation. The picture is then something like a steady state universe ‘in the large’, where uphill quantum fluctuations continously replenish the inflating regions, so that the production of ‘island Universes’ continues indefinitely.
Figure
1: De Sitter spacetime is a four dimensional
hyperboloid
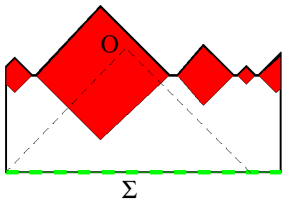
Figure 2: Causal diagram showing the formation of ‘bubble universes’ within de Sitter space. de Sitter spacetime is represented as the surface of a two dimensional cylinder (here seen from the side) where the circular cross sections are actually three spheres. The special three sphere Σ is the equator or initial condition surface for de Sitter space. The point O represents the location of an observer inside one of the bubble Universes. The past light cone does not intersect any of the other bubble Universes. We do not have the techniques to fully verify this behavior not least because there is no consistent theory of quantum gravity we can use to perform the calculation. But in spite of this there are various approximate calculations we can perform and there is a fair amount of evidence that the basic physical picture is correct. Jumps of φ uphill lead to exponential expansion because they increase the potential energy V(φ) increasing its repulsive effect. Nevertheless I believe there is a serious flaw in the reasoning, which renders the eternal inflation effect irrelevant. The problem is that the argument neglects the constraint of causality. We are all used to the fact that an event can only be said to be ‘caused’ by something which precedes it. In relativity theory, causality is a stronger constraint because nothing travels faster than the speed of light. Thus something can only be ‘caused’ by phenomena within a certain distance from it, roughly the speed of light times the time before the event. This region of space-time is called the past light cone of the event. All the laws of physics we know (general relativity and quantum field theory) are consistent with causality in this form. Causality implies that all measurable quantities (more precisely, all correlators) at a set of spacetime points {x} are fully determined by the complete set of measureable quantities (equivalently, correlators) evaluated on a space-like surface which fills the past light cones of all of the points {x} in question. Figures (1) and (2) show how causality works in an inflating spacetime. The solution of the field equations in general relativity with a positive cosmological constant is called de Sitter spacetime. It has the geometry of a four dimensional hyperboloid embedded in five dimensional Minkowski spacetime Figure (1). For example, if we start the Universe on a three-sphere which is static (i.e. not expanding) then it will expand due to the repulsive effect of the cosmological constant. The slice Σ of the spacetime (which is a three-sphere) grows exponentially, as we go forward or backwards in time due to this effect. The diagram also shows that de Sitter spacetime can be time-sliced as a closed Universe, a flat Universe or an open Universe. This illustrates the point that ‘three-volume’, whilst an intuitive concept, is actually hard to define. If we speak of our initial inflating region expanding its volume by some amount, we need to specify which spatial slicing we use. By changing the slicing, we can completely change the inferred volume, by an infinite amount. The second diagram, Figure (2), shows the causal properties of de Sitter spacetime. In this diagram, physical length and time scales have been shrunk so that the whole of the spacetime is now a finite region. The infinite hyperboloid shown in Figure (1) is shrunk to a finite cylinder S3 times an interval. In fact only the region to the future of the initial surface Σ is shown, for reasons which will be explained below. The important point however is that in the causal diagram Figure (2), light rays move at +/- 45o to the vertical. Now let us consider the production of island hot big bang Universes within the inflating spacetime. This description is relatively well understood in the case where the scalar field is trapped in a metastable minimum of its potential and out of which it quantum tunnels. The tunneling has the effect of causing bubbles to nucleate inside of which the field rolls down the potential to the true minimum (assumed to be at V = 0). Outside the bubbles the field is nearly constant and the spacetime is near perfect de Sitter spacetime. The interior of the bubble is the region inside the future lightcone of
the nucleation point. For example, a bubble nucleating on the surface labeled
Σ is bounded by a spherical bubble wall which grows out along the light
cone indicated by the solid vertical line on the right of the diagram. It is a remarkable fact that the surfaces of
constant field Φ, which are also the surfaces of
constant energy density turn out to be the open
slices of de Sitter spacetime. These
slices turn into the natural ‘constant time’ slices in the ensuing hot big
bang. Remarkably therefore, an infinite
open universe is contained in the spacetime future of a perfectly finite
bubble. Thus we see the first emergence of an infinity - the spatial regions undergoing heating following
inflation are in fact infinite open universes. The existence of these infinities of infinite Universes presents a real problem, which simply put is the question ‘Where are we?’. It is not clear what the relative probability is to be in one part of an island Universe as opposed to another, or in one bubble or another. This lack of predictivity leads to what Vilenkin has termed the ‘predictability crisis’ in inflation. Let me expand briefly on what this crisis is. We are only expecting to be able to calculate relative probabilities for different types of Universes, since that is all quantum theory allows us to consider. Relative probabilities are always well defined when the number of distinct possibilities is finite. For example if one takes a card from the top of a well-shuffled pack, one expects to get a heart or a club with equal probabilities. Likewise we could take many packs and keep more clubs than hearts to bias the probabilities, but as long as there were a finite total number of cards there would always be a well defined probability, given a random choice of card. The situation becomes more difficult when there are an infinite number of possibilities. We cannot enumerate all the possible orderings and it is hard to say which are more probable than others. For example, take all the integers from one to infinity. If we put all the odd numbers first, it might appear that a number chosen at random would have to be odd. With the even even numbers put first we would reach the opposite conclusion (this example has been used by Guth). We need to define the relative probabilities more carefully, and in such a way that the infinities are taken care of. It seems to me that the original question of what an eternally inflating spacetime looks like is actually the wrong question. We should not ask ‘where are we?’ in the infinite, quantum fluctuaing spacetime. Rather we should note that causality implies the only parts of the spacetime that ever influence what we see are the parts inside our past light cone. An example is shown in Figure (2). An observer at O, inside a bubble, is causally disconnected from events in bubbles which never collide with that bubble. For an observer living inside a bubble, everything observable now or in the future should be fully determined by the physics inside her/his past light cone. It should be completely unnecessary to discuss the other bubbles. The constraint of causality is very important because in a stroke it removes the twin problems of an infinite number of infinite open universes, leaving us with a much better defined problem. The question of what an inflating spacetime looks like should therefore be re-phrased. We should ask ‘Given that we have undergone a hot big bang, what is the most probable past within our past light cone?’
Contributed by: Dr. Neil Turok |
 embedded in five
dimensional Minkowski spacetime. A two dimensional version is illustrated,
embedded in three-dimensional Minkowski spacetime. It may be time-sliced on closed, flat or open slices as shown. In
four-dimensional de Sitter spacetime the closed slices are three spheres and
the open slices are three dimensional hyperbolic spaces, or infinite open
universes. The heavy vertical line (dotted
on the rear side) represents the
embedded in five
dimensional Minkowski spacetime. A two dimensional version is illustrated,
embedded in three-dimensional Minkowski spacetime. It may be time-sliced on closed, flat or open slices as shown. In
four-dimensional de Sitter spacetime the closed slices are three spheres and
the open slices are three dimensional hyperbolic spaces, or infinite open
universes. The heavy vertical line (dotted
on the rear side) represents the